Introuction
Constrained Many-Body Systems and Related Lattice Gauge Theory
The local constraints emerging in frustrated quantum magnets or blocked cold atom systems would induce novel phases, such as topological order, fracton phase and incommensurate region. We feel interested in the related models, such as the frustrated quantum Ising/XXZ model, the X-cube/Toric code model and the quantum dimer/loop model. We pay close attention to the novel phases, fractional excitations and critical behaviors in them. We also combine relevant experiments to make predictions and explanations.
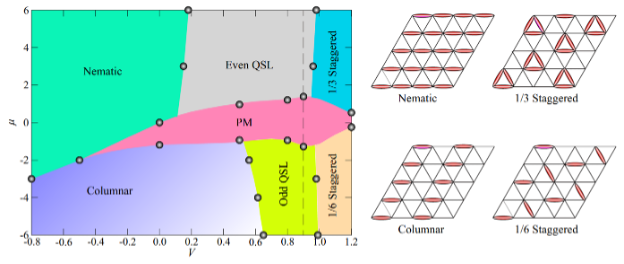
Figure1: A phase diagram including both the even and odd quantum spin liquids in an extended quantum dimer model with a soft constraint. (From: Nat. Commun. 13, 5799 (2022))
Quantum Simulation/Computation
We, on one hand, focus on the numerical prediction/explanation of simulating nontrivial many-body physics via a Rydberg array and optical lattice system. On the other hand, we also feel interested in the approaches/algorithms for optimization problems through practical quantum simulators/circuits.
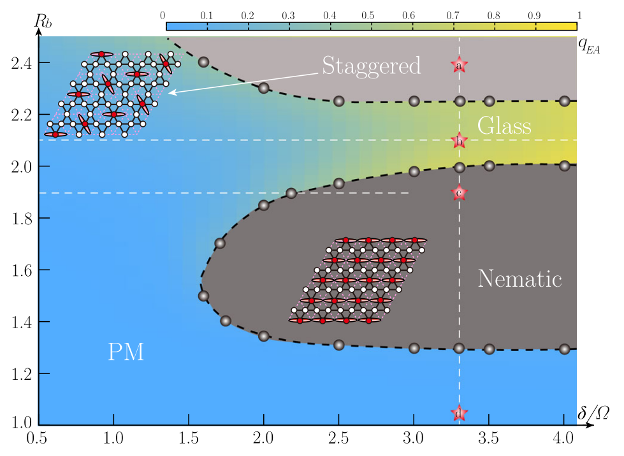
Figure 2: A glassy region emerges in a Kagome Rydberg array. (From:Phys. Rev. Lett. 130, 206501 (2023))
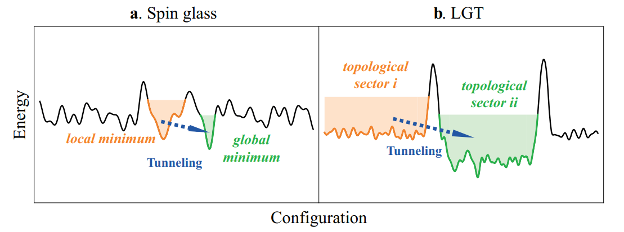
Figure 3: A new experimental scheme to overcome the topological obstructions in an optimization problem. (From: npj Quantum Inf. 9, 89 (2023))
Quantum Many-Body Entanglement
We concern about how to use entanglement measurements to extract the information from condensed matter systems and the mechanisms behind these entanglement qualities. We are also interested in the connection between many-body entanglement and quantum information.
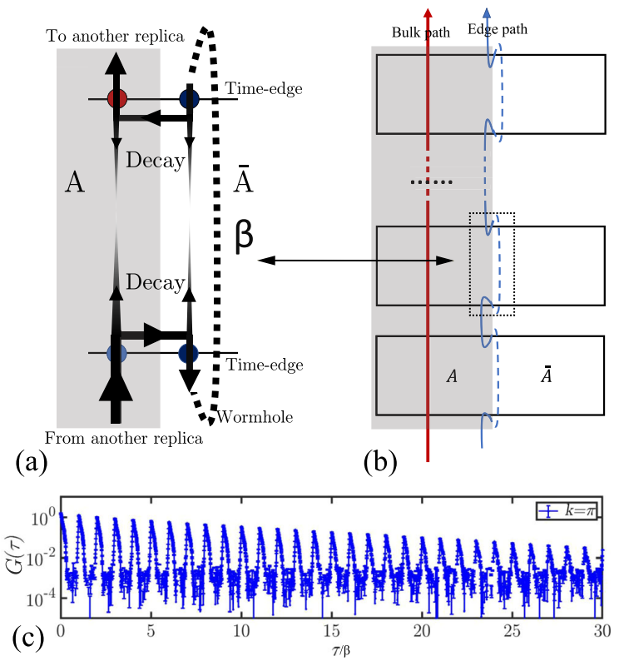
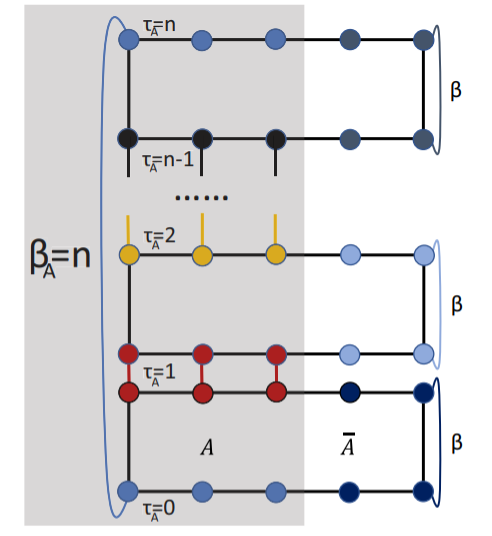
Figure 4: The wormhole effect in the path integral of the reduced density matrix to unlock the mechanism of the entanglement spectrum. (From: Nat. Commun. 14, 2360 (2023))
Developing Advanced Numerical Methods for Many-Body System
We also work hard to extend the scope of numerical methods to explore more many-body systems and observables. Now we are mainly focusing on the quantum Monte Carlo algorithm and its combined usage with exact diagonalization. In addition, we are paying great efforts to reduce the sign problem to make the quantum Monte Carlo algorithm more powerful. Certainly, we are willing to try more numerical tools.
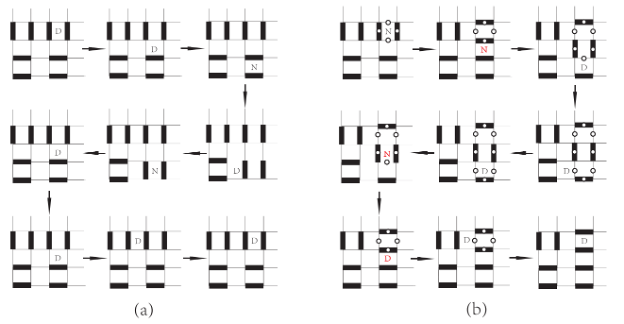
Figure 5: The sweeping cluster quantum Monte Carlo algorithm solving the simulation problem of local constrained models. (From: Phys. Rev. B 99, 165135 (2019)) The method has been included in an international textbook 《Many-Body Methods for Real Materials》 as a single subsection.